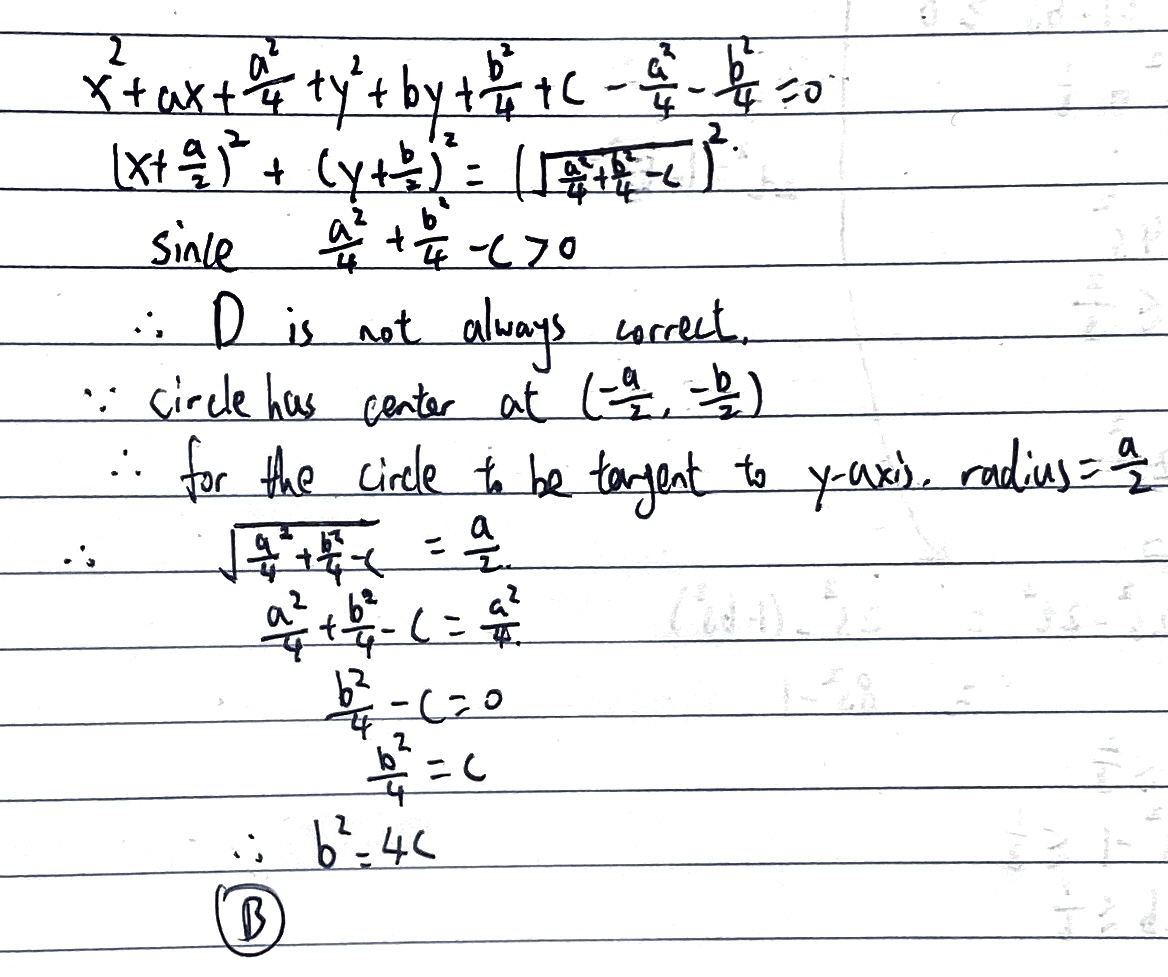Term 1 Week 9 Senior Problems
Problem 1
The smallest possible integer $n$ such that
\[1-2+3-4+5-6+\cdots+(-1)^{n+1}n\ge100,\]is
\[\textbf{(a)}\ 99\qquad\textbf{(b)}\ 101\qquad\textbf{(c)}\ 199\qquad\textbf{(d)}\ 300\]Click to show solution
Summing the first few terms of the series $$ 1-2+3-4+5-6+\cdots+(-1)^{n+1}n, $$ we see that we get the sequence $$ 1,-1,2,-2,3,-3,4,-4,5,-5,6,-6,\cdots, $$ The first time this equals to or exceeds $100$ is when $n = 199$$\therefore$ the answer is $\boxed{(c)}$
Problem 2
In how many ways can three different numbers be selected from the integers $1, 2, 3, \cdots , 23, 24$ so that their sum is exactly divisible by $3$?
Click to show solution
The numbers can be divided into three sets of $8$, such that in the first set we have the numbers 0 mod 3, in the second set we have the numbers 1 mod 3 and in the third set we have the numbers 2 mod 3. That is to say, the first set contains $3,6,9,\cdots,24$. the second contains $1,4,7,\cdots,22$, and the third contains $2,5,\cdots,23$. A sum of three numbers divisible by three can be done four wavs. You can take three numbers from one set, (and there are $3$ sets), or one number from each of the three sets. Taking three distinct numbers from a set can be done in $8$ choose $3$ = 56 ways. Choosing one number from each set can be done in $8^3$ = 512 wavs. So the total number of wavs is $3 \times 56 + 512 = 680$Problem 3
\(\begin{gathered}
a+b+c=0 \\
a^{2}+b^{2}+c^{2}=1
\end{gathered}\)
Proof: $a^{2} b^{2} c^{2} \leq \frac{1}{54}$
Hint: let $a=s+t, b=s-t, c=-2 s$
Click to show solution
Solution
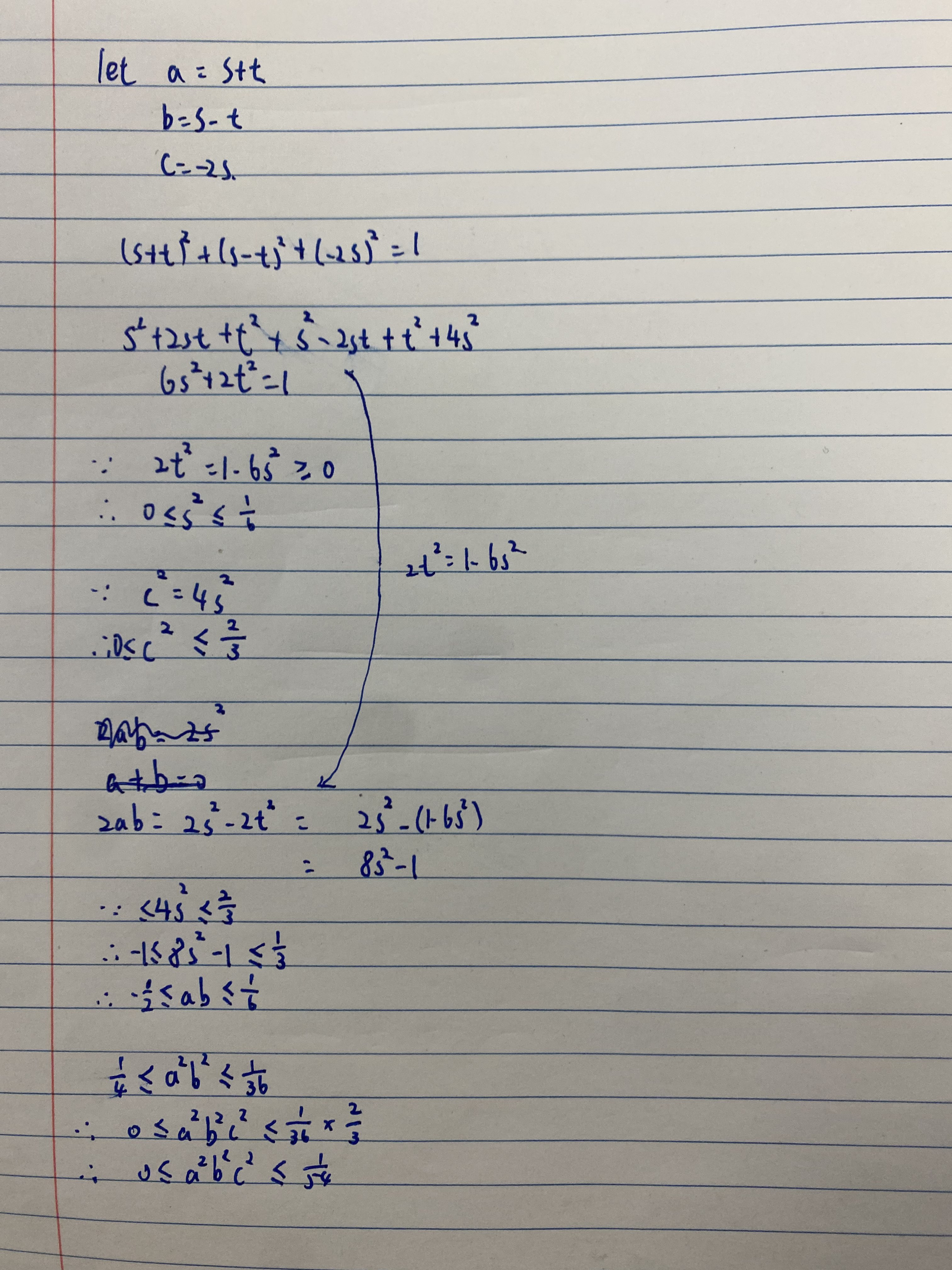
Problem 4
A circle has equation
\(x^{2}+a x+y^{2}+b y+c=0\)
where $a, b$ and $c$ are non-zero real constants.
Which one of the following is a necessary and sufficient condition for the circle to be tangent to the $y$-axis?
A. $a^{2}=4 c$
B. $b^{2}=4 c$
C. $\frac{a}{2}=\sqrt{\frac{a^{2}+b^{2}}{4}-c}$
D. $\frac{b}{2}=\sqrt{\frac{a^{2}+b^{2}}{4}-c}$
E. $-\frac{a}{2}=\sqrt{\frac{a^{2}+b^{2}}{4}-c}$
F. $-\frac{b}{2}=\sqrt{\frac{a^{2}+b^{2}}{4}-c}$
Click to show solution
Solution