Term 2 Week 9 Junior Problems
Problem 1
Triangular numbers are those numbers that can be represented geometrically as a triangle, as shown in the image below:
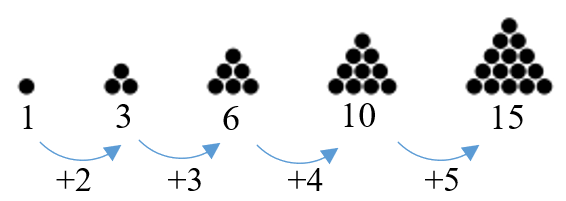
The $n^{th}$ triangular number is equal to $1+2+3+…+n$.
It can also be evaluated using the very useful formula $\dfrac{n(n+1)}{2}$.
The last year that was a triangular number was 2016. What is the next year that is a triangular number?
Click to show solution
Answer: 2080
The formula $\dfrac{n(n+1)}{2}$ is very useful. By trial and error, we can find that $2016=\dfrac{63 \times 64}{2}$. The next triangular year is $\dfrac{64 \times 65}{2}=2080$.
Problem 2
Madeleine types her three-digit Personal Identification Number (PIN) into this keypad.
All three digits are different, but the buttons for the first and second digits share an edge, and the buttons for the second and third digits share an edge.
For instance, 563 is a possible PIN, but 536 is not, since 5 and 3 do not share an edge.
How many possibilities are there for Madeleine’s PIN?

Click to show solution
Answer: 50
The three digits must make one of the following shapes on the keypad. Below each shape, the number represents the number of ways in which the shape can be placed on the keypad.
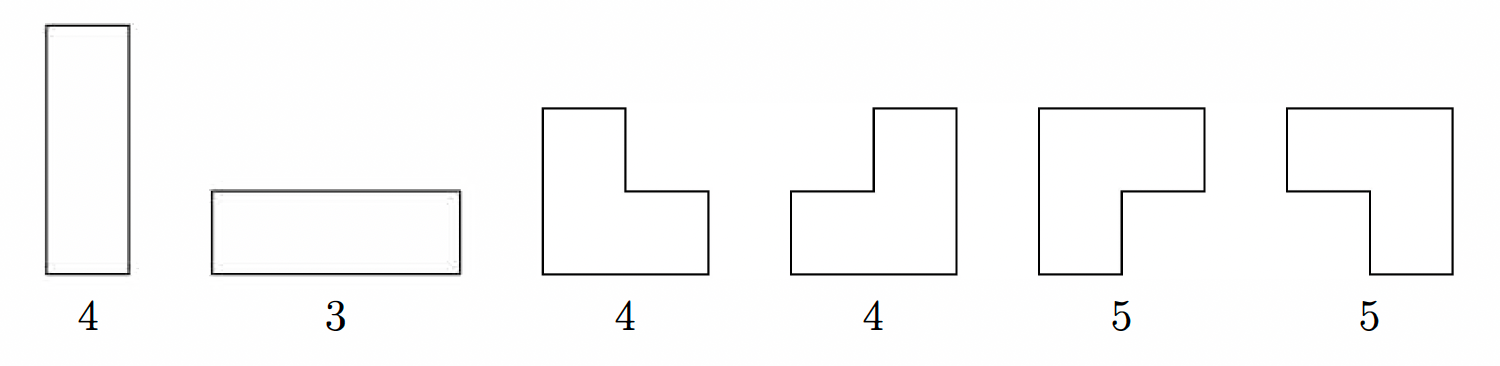
For each such shape, there are two possible Personal Identification Numbers. So the number of possibilities for Madeleine's PIN is:
$2\times(4 + 3 + 4 + 4 + 5 + 5) = 50$