Term 1 Week 8 Junior Problems

23 Mar 2022

Problem 1

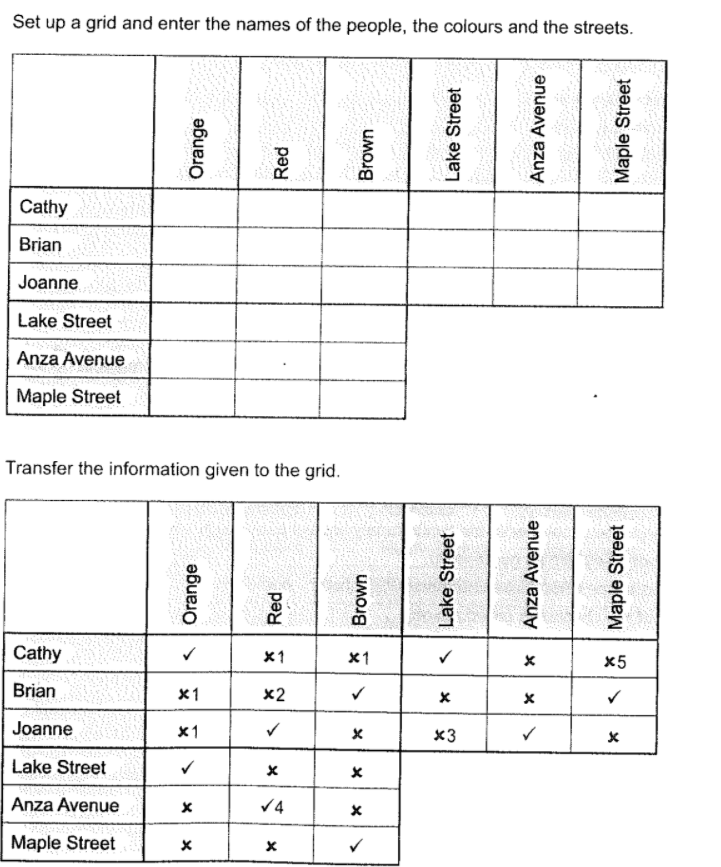
Three children live in different coloured houses on three different streets.

1. Cathy’s house is orange.
2. Brian’s house does not have a red door.
3. Joanne does not live in Lake Street.
4. In Anza Avenue, everyone has a red house.
5. Cathy does not live in Maple Street.
6. Someone lives in a brown house.

Find out the name of the street and the colour of each child’s house.

Click to show solution

Solution

Problem 2

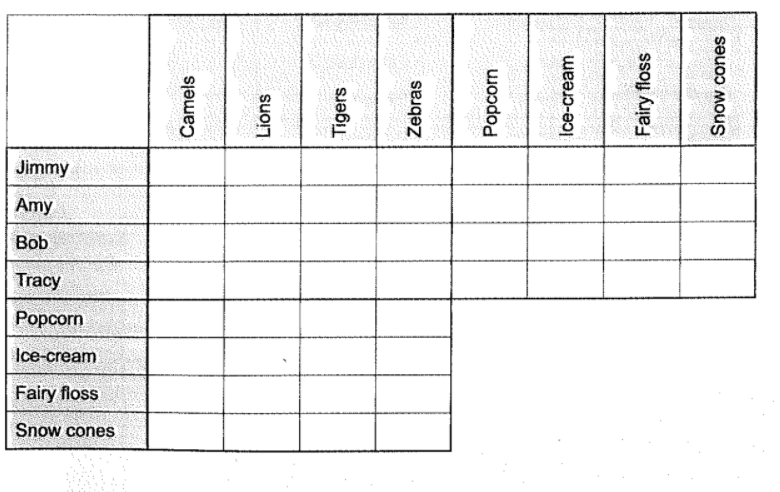
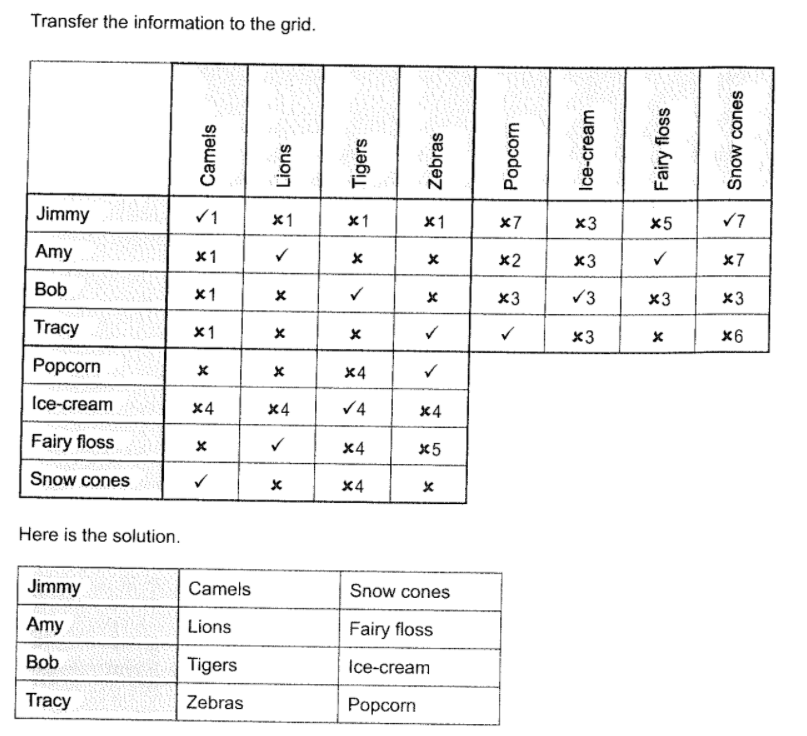
Four children go to see the circus. Each child has a favourite circus animal, and each one likes a certain circus food. Each child’s choice is different.

1. Jimmy likes camels.
2. Amy hates popcorn.
3. Bob likes ice-cream.
4. One person eats an ice-cream while enjoying the tigers.
5. The person who likes zebras hates fairy floss.
6. Amy hates snow cones.
7. The boy who eats snow cones hates lions.

Find out the children’s names, their favourite animals, and the food they like.

Click to show solution

Solution

Problem 3

Determine all natural numbers $n$, such that it’s possible to insert one digit on the right side of $n$ to obtain $13n$.

Click to show solution

Solution

Assume the number to be $abc \cdots m$. We see that the new number is $10*n+x$ where $x$ is $0$ to $9$, so we see that $3n$ is less $10$. So we see that $n$ is $0,1,2,3$

Problem 4

Let $a$ and $b$ be real numbers such that $\frac{a}{b} + \frac{b}{a} = 3$. Evaluate $(\frac{a+b}{a-b})^5$

Click to show solution

Solution

$\frac{a}{b}+\frac{b}{a}=3$, so $a^2+b^2=3ab$. $(a+b)^2=5ab$, and $(a-b)^2=ab$. So $(a+b)=\pm \sqrt{5ab}$ and $(a-b)=\pm \sqrt{ab}$. Now with $ab$, it is much easier, we have $\frac{25(ab)^2\sqrt{5ab}}{(ab)^2\sqrt{ab}}=25\sqrt{5}$ as the answer

Credits:

Problem 1: Joseph Hartono

Problem 2: Joseph Hartono

Problem 3: This problem is from the Polish Junior Math Olympiad 2020 First Round

Problem 4: This problem is by twinbrain