Term 2 Week 2 Junior Problems
Problem 1
Find the smallest multiple of nine containing only even digits.
Click to show solution
If a number is divisible by nine then the sum of digits must be a multiple of nine.But if all of the digits are even then they must sum to an even multiple of nine, and the smallest even multiple of nine is eighteen.
Hence we are looking for the most efficient way to write eighteen as the sum of even digits: 2 + 8 + 8. That is, the smallest multiple of nine containing only even digits is 288.
Find the first five multiples of nine containing only even digits.
Problem 2
The sum of the first $n$ squares, $1^2 + 2^2 + \cdots + n^2 = \frac{n(n+1)(2n+1)}{6}$.
For example, $1^2 + 2^2 + \cdots + 10^2 = \frac{10 \times 11 \times 21}{6} = 385$.
Prove that $n(n+1)(2n+1)$ is divisible by six for all integer values, $n$.
Click to show solution
To prove that $n(n+1)(2n+1)$ is divisible by $6$ we must show that it is divisible by both $2$ and $3$.As $n$ and $n+1$ are consecutive integers then exactly one of them will be even and thus divisible by $2$.
If neither $n$ nor $n+1$ is divisible by $3$ then $n+2$ will be. Therefore $2(n+2)=2n+4$ and $2n+4-3=2n+1$ will be divisible by $3$.
Hence $n(n+1)(2n+1)$ is divisible by both $2$ and $3$.
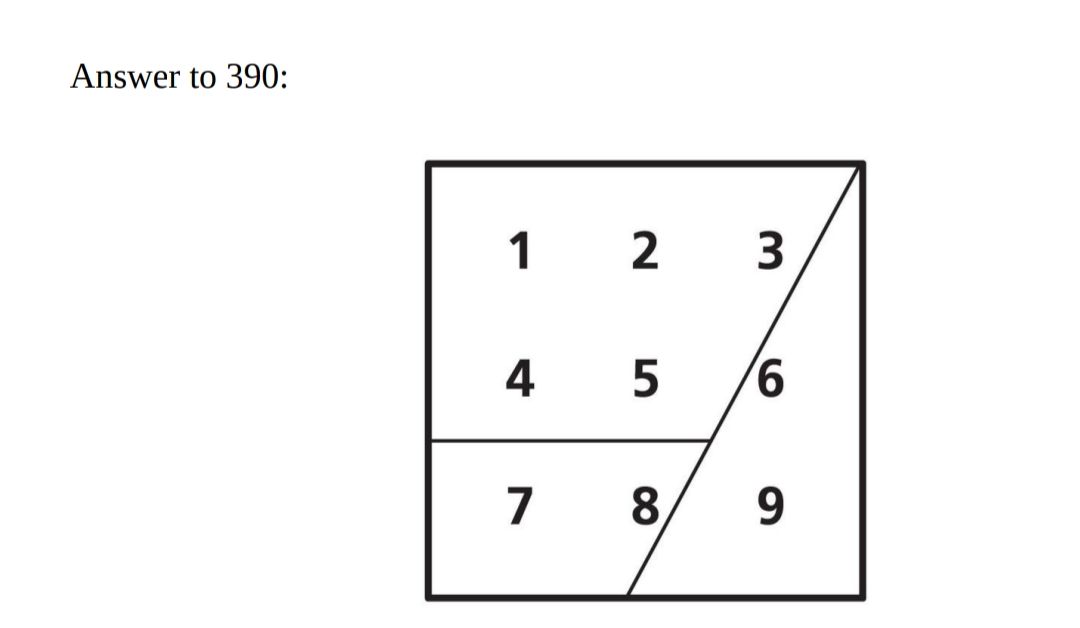
Problem 3

Click to show solution
Solution
Problem 4

Click to show solution
Solution