Term 1 Week 10 Junior Problems
Problem 1
Bob , Alice, and Tim decided to play ping pong. Only two people can play at a time, so they agree that two of them will start playing, and then whoever loses the game will swap out with the player who was sitting out.
Bob played $17$ games, Alice played $15$ games, and Tim played $10$ games.
Who lost the second game?
Click to show solution
Solution
21 games were played, with one person sitting out each time. The person who lost the second game sat out for the third. Note that no one can sit out two games in a row. Tim sat out for 11 games, which must have been games 1,3,5,...,21. Thus Tim lost the second game to sit out the third.Problem 2
Show that $1999^{1999}<(1999!)^2$
Click to show solution
By flipping one of the factorials and interleaving the factors, we can express $1999!2 = (1\times1999) \times (2\times1998) \times (3\times1997) \times \cdots \times (1998\times2) \times (1999\times1)$. This expression has $1999$ sub-factors (e.g. $3\times1997$ is one sub-factor). All of them are greater than or equal to $1999$, hence the product has to be greater than $1999^{1999}$.Problems 3 & 4
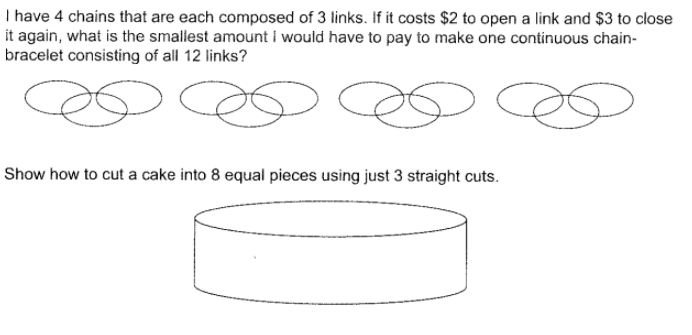
Click to show solution
Question 3 Solution
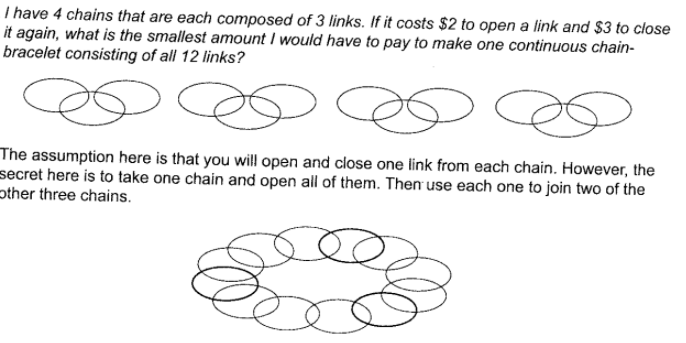
Question 4 Solution